Next: Quantum algorithms Up: libquantum 1.1.1 API documentation Previous: Quantum registers
To manipulate quantum registers and to implement quantum algorithms, libquantum provides a set of function for quantum register manipulation by quantum gates. Each gate is called via a common interface:
| quantum_NAME(QUBIT[S], [PARAMETER], ®ISTER); |
NAME is the name of the gate, QUBIT[S] are one ore more integers describing the Qubits that are relevant for the operation. All qubits are given in a notation starting with 0 as the least significant bit. Some functions require an additional PARAMETER, e.g. an angle of a rotation. ®ISTER contains the address of the quantum register.
| extern void quantum_cnot(int control, int target, quantum_reg *reg); |
This function performs a controlled not operation. The target bit gets
inverted if the control bit is enabled. The operation can be written
as the unitary operation matrix
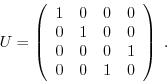
| extern void quantum_toffoli(int control1, int control2, int target, quantum_reg *reg); |
This operation is a controlled-not with two controlling qubits. The
unitary operation matrix is

| extern void quantum_unbounded_toffoli(int controlling, quantum_reg *reg, ...); |
An unbounded Toffoli gate is a controlled-not operation with an arbritrary number of controlling qubits. This gate is not considered elementary and is not available on all physical realizations of a quantum computer. Be sure that controlling contains the correct number of controlling qubits. The last argument contains the target qubit.
|
extern void quantum_sigma_x(int target, quantum_reg *reg);
extern void quantum_sigma_y(int target, quantum_reg *reg); extern void quantum_sigma_z(int target, quantum_reg *reg); |
These functions perform the Pauli spin operations, defined as
Note that the ![]() operation is the same as a not operation.
operation is the same as a not operation.
|
extern void quantum_r_x(int target, float gamma, quantum_reg *reg);
extern void quantum_r_y(int target, float gamma, quantum_reg *reg); extern void quantum_r_z(int target, float gamma, quantum_reg *reg); |
These functions perform a rotation of a qubit about an axis of the
Bloch sphere. The angle of the rotation is given by gamma. The
rotations can be described by their unitary operation matrices
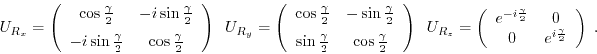
| extern void quantum_phase_scale(int target, float gamma, quantum_reg *reg); |
This function adds a global phase on a qubit, as shown in its unitary
operation matrix
| extern void quantum_phase_kick(int target, float gamma, quantum_reg *reg); |
This function performs a phase kick or phase shift. It is described by
the unitary operation matrix
| extern void quantum_hadamard(int target, quantum_reg *reg); |
This function provides the widely used Hadamard gate. The Hadamard
gate can establish or destroy the superposition of a qubit. The unitary
operation matrix is defined as
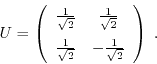
| extern void quantum_walsh(int width, quantum_reg *reg); |
The Walsh-Hadamard transform consists of Hadamard gates applied on the first width qubits of the quantum register.
| extern void quantum_cond_phase(int control, int target, quantum_reg *reg); |
This function performs a conditional phase shift. It is a controlled
phase kick about the angle
![]() with
with
![]() . The unitary operation matrix is
. The unitary operation matrix is
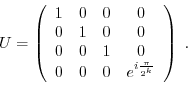
| extern void quantum_cond_phase_kick(int control, int target, float gamma, quantum_reg *reg); |
This function does a phase kick on the target bit about the
angle gamma, controlled by control. The unitary operation
matrix is defined as
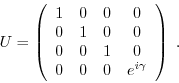
| extern void quantum_gate1(int target, quantum_matrix m, quantum_reg *reg); |
This function provides an interface for arbitrary 1-bit operations. The operation matrix is given in the following structure:
|
quantum_matrix
{ int rows; int cols; COMPLEX_FLOAT *t; }; |
The elements of a matrix m are arranged as follows:
![\begin{displaymath}\left(\begin{array}{cc}
m.t[0] & m.t[1]\vspace{0.2cm}\\
m.t[2] & m.t[3]\end{array}\right)\end{displaymath}](img31.png)
New matrices can be created using quantum_new_matrix:
| extern quantum_matrix quantum_new_matrix(int cols, int rows); |
To delete a matrix and free its allocated memory, use quantum_delete_matrix:
| extern void quantum_delete_matrix(quantum_matrix *m); |
| extern void quantum_gate2(int target1, int target2, quantum_matrix m, quantum_reg *reg); |
Provides arbitrary two-bit gates. The parameters are identical to those to quantum_gate1, except that the matrix acts on two qubits, target1 and target2.