Next: Basic quantum operations Up: libquantum 1.1.1 API documentation Previous: Introduction
All quantum computation is done with quantum registers. libquantum provides a structure for a quantum register:
|
quantum_reg
{ int width; /* number of qubits in the register */ int size; /* number of non-zero vectors */ int hashw; /* width of the hash array */ COMPLEX_FLOAT *amplitude; MAX_UNSIGNED state; int *hash; }; |
To achieve an efficient memory usage, the quantum register can be used
in a sparse configuration by containing only the basis vectors
with a non-zero probability amplitude. In this case, state is
non-NULL and points to an array containing the non-zero basis
states. This implementation is equivalent to the widely used
description of a quantum state vector ![]() with
with
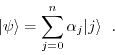
In this case, amplitude[j] is ![]() and state[j] is
and state[j] is
![]() . If state is NULL, then
. If state is NULL, then ![]() runs over all
runs over all ![]() basis states. Note that
quantum_new_qureg
and
quantum_new_qureg_sparse
create sparse registers, while
quantum_new_qureg_size
does not.
basis states. Note that
quantum_new_qureg
and
quantum_new_qureg_sparse
create sparse registers, while
quantum_new_qureg_size
does not.
| extern quantum_reg quantum_new_qureg(MAX_UNSIGNED initval, int width); |
This function is used to create a quantum register. initval contains the value to which the register is initialized at the beginning. On most machines, it is a 64-bit integer. width contains the number of qubits the register should start with. Note that the size of the hash table is computed according to this value, so additional scratch space should be added later with quantum_addscratch.
| extern quantum_reg quantum_new_qureg_size(int n, int width); |
This function creates an empty non-sparse quantum register with n basis states for width qubits. Filling the amplitude array with values lies within your responsibility.
| extern quantum_reg quantum_new_qureg_sparse(int n, int width); |
This is a variant of quantum_new_qureg_size creating a sparse quantum register. Again, populating the amplitude and state arrays lies within your responsibility. This function is particularly useful for creating a quantum register that is returned by a function implementing a Hamiltonian.
| extern void quantum_delete_qureg(quantum_reg *reg); |
Deletes a quantum register and frees its allocated memory.
| extern void quantum_print_qureg(quantum_reg reg); |
Prints the contents of a quantum register to the standard output stream.
| extern void quantum_addscratch(int bits, quantum_reg *reg); |
This function adds bits of scratch space to a quantum
register. The scratch space is initialized to zero and gets inserted
at the least significant bit of the register, i.e. the register
changes from ![]() to
to
![]() . Note that this space
is not included for computing the size of the hash table, so creating
new basis states in the scratch space will overfill the hash table.
. Note that this space
is not included for computing the size of the hash table, so creating
new basis states in the scratch space will overfill the hash table.
| extern quantum_reg quantum_kronecker(quantum_reg *reg1, quantum_reg *reg2); |
This function creates the Kronecker product of two registers. The target register is linked with the control registers by the following scheme:
Suppose ![]() is a
is a ![]() -lined vector and
-lined vector and ![]() is a
is a ![]() -lined vector,
then we have the representation
-lined vector,
then we have the representation
![\begin{displaymath}
\vert A\rangle \otimes \vert B\rangle \equiv
\left[ \begin...
... A_1 B_2 ... A_{2^n} B_{2^m}
\end{array} \right] \; . \end{displaymath}](img15.png)
| COMPLEX_FLOAT quantum_dot_product(quantum_reg *reg1, quantum_reg *reg2); |
Computes the dot product of two quantum registers. Let
![]() and
and
![]() denote the two quantum registers reg1 and
reg2, respectively, then the dot product is
denote the two quantum registers reg1 and
reg2, respectively, then the dot product is